文章目录
第一部分:回归栗子
ps:CP3的部分在上一篇笔记中【李宏毅机器学习】CP1-3笔记了。
1.问题描述
现在假设有10个x_data和y_data,x和y之间的关系是
y
d
a
t
a
=
b
+
w
?
(
x
d
a
t
a
)
ydata=b+w*(xdata)
ydata=b+w?(xdata)b,w都是参数,是需要学习出来的。现在我们来练习用梯度下降找到b和w。
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
# matplotlib没有中文字体,动态解决
plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
arange,numpy.arange(start, stop, step, dtype = None)生成数组
值在半开区间 [开始,停止]内生成(换句话说,包括开始但不包括停止的区间),返回的是 ndarray 。
x = np.arange(-200, -100, 1)
y = np.arange(-5, 5, 0.1)
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)
2.利用梯度下降寻找最优参数
# loss
for i in range(len(x)):
for j in range(len(y)):
b = x[i]
w = y[j]
Z[j][i] = 0 # meshgrid吐出结果:y为行,x为列
for n in range(len(x_data)):
Z[j][i] += (y_data[n] - b - w * x_data[n]) ** 2
Z[j][i] /= len(x_data)
先给b和w一个初始值(先设定b=-120,w=-4),计算出b和w的偏微分,迭代更新b和w值,实现根据梯度下降寻找loss值最低点。
# linear regression
b = -120
w = -4
#b=-2
#w=0.01
lr = 0.0000001
iteration = 100000
b_history = [b]
w_history = [w]
loss_history = []
import time
start = time.time()
for i in range(iteration):
m = float(len(x_d))
y_hat = w * x_d +b
loss = np.dot(y_d - y_hat, y_d - y_hat) / m
grad_b = -2.0 * np.sum(y_d - y_hat) / m
grad_w = -2.0 * np.dot(y_d - y_hat, x_d) / m
# update param
b -= lr * grad_b
w -= lr * grad_w
b_history.append(b)
w_history.append(w)
loss_history.append(loss)
if i % 10000 == 0:
print("Step %i, w: %0.4f, b: %.4f, Loss: %.4f" % (i, w, b, loss))
end = time.time()
print("大约需要时间:",end-start)
输出的结果为:
Step 0, w: 1.6534, b: -119.9839, Loss: 3670819.0000
Step 10000, w: 2.4781, b: -121.8628, Loss: 11428.6652
Step 20000, w: 2.4834, b: -123.6924, Loss: 11361.7161
Step 30000, w: 2.4885, b: -125.4716, Loss: 11298.3964
Step 40000, w: 2.4935, b: -127.2020, Loss: 11238.5092
Step 50000, w: 2.4983, b: -128.8848, Loss: 11181.8685
Step 60000, w: 2.5030, b: -130.5213, Loss: 11128.2983
Step 70000, w: 2.5076, b: -132.1129, Loss: 11077.6321
Step 80000, w: 2.5120, b: -133.6607, Loss: 11029.7126
Step 90000, w: 2.5164, b: -135.1660, Loss: 10984.3908
大约需要时间: 1.8699753284454346
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
# 标记最优解的位置为橙色的X符号
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
# 标记迭代过程中的线条为黑色线
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)# 定义直方图的横纵坐标的范围
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()
输出结果如图

横坐标是b,纵坐标是w,标记×位(上图的橙色叉叉)最优解,显然,在图中我们并没有运行得到最优解,最优解十分的遥远。那么我们就调大learning rate,lr = 0.000001(调大10倍),得到结果如下图,发现还不如一开始的lr值效果好。

我们再调大learning rate,lr = 0.00001(调大10倍),得到结果如下图,发现更加接近最优解了,但是在b=-120的这条竖线往上随着迭代过程中出现剧烈震荡的现象:

结果发现learning rate太大了,结果很不好。
3.给b和w特制化两种learning rate
所以我们给b和w特制化两种learning rate
# linear regression
b = -120
w = -4
lr = 1
iteration = 100000
b_history = [b]
w_history = [w]
lr_b=0
lr_w=0
import time
start = time.time()
for i in range(iteration):
b_grad=0.0
w_grad=0.0
for n in range(len(x_data)):
b_grad=b_grad-2.0*(y_data[n]-n-w*x_data[n])*1.0
w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
lr_b=lr_b+b_grad**2
lr_w=lr_w+w_grad**2
# update param
b -= lr/np.sqrt(lr_b) * b_grad
w -= lr /np.sqrt(lr_w) * w_grad
b_history.append(b)
w_history.append(w)
# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet')) # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()

有了新的特制化两种learning rate就可以在10w次迭代之内到达最优点了。
第二部分:Python Basics with Numpy
该内容来自吴恩达的task2的numpy练习
- Avoid using for-loops and while-loops, unless you are explicitly told to do so.就是少用或者不用循环,防止时间复杂度过高。
- math库的方法输入一般是实数,而numpy输入一般是矩阵或者向量,所以numpy更适合DL
- 在anaconda jupyter上运行代码只需要shift+enter;如果如要查询文档,如np.exp的详解,就直接开一个新的cell写
np.exp?即可。或者看官方文档:https://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.exp.html
0.目标:
- Be able to use numpy functions and numpy matrix/vector operations
- 理解广播 “broadcasting”
- Be able to vectorize code
1.用numpy建立基本函数
1)sigmoid函数
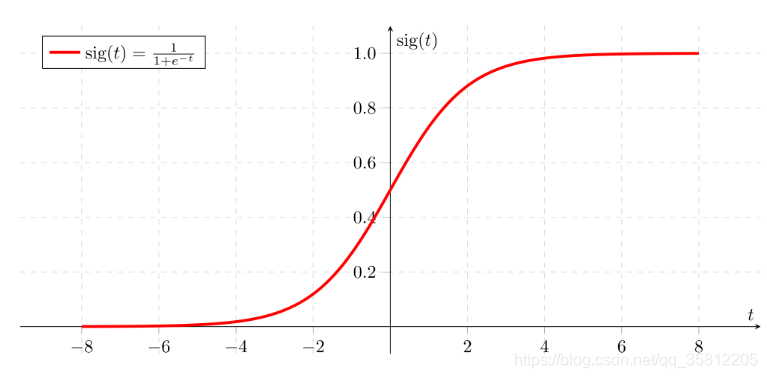
先用math.exp()实现sigmoid函数——一种非线性的逻辑函数(计算公式如下),不仅在机器学习中的逻辑回归,在深度学习中也会用作激活函数。
sigmoid函数用于隐层神经元输出,取值范围为(0,1),可以将一个实数映射到(0,1)的区间,可以用来做二分类。
- 优点:平滑,易于求导
- 缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,容易出现梯度消失的情况(从而无法完成深层网络的训练)。
sigmoid ? ( x ) = 1 1 + e ? x \operatorname{sigmoid}(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e?x1?
ps:使用包的用法package_name.function(),如math.exp()。
import math
# from public_tests import *
# GRADED FUNCTION: basic_sigmoid
def basic_sigmoid(x):
"""
Compute sigmoid of x.
Arguments:
x -- A scalar
Return:
s -- sigmoid(x)
"""
# (≈ 1 line of code)
# s =
# YOUR CODE STARTS HERE
s = 1/(1 + math.exp(-x))
# YOUR CODE ENDS HERE
return s
print("basic_sigmoid(1) = " + str(basic_sigmoid(1)))
# 打印输出basic_sigmoid(1) = 0.7310585786300049
numpy输入一般是矩阵或向量,实数当然也可以:
### One reason why we use "numpy" instead of "math" in Deep Learning ###
x = [1, 2, 3]
basic_sigmoid(x) # you will see this give an error when you run it, because x is a
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-6-8ccefa5bf989> in <module>()
1 ### One reason why we use "numpy" instead of "math" in Deep Learning ###
2 x = [1, 2, 3]
----> 3 basic_sigmoid(x) # you will see this give an error when you run it, because x is a vector.
<ipython-input-3-28be2b65a92e> in basic_sigmoid(x)
15
16 ### START CODE HERE ### (≈ 1 line of code)
---> 17 s = 1/(1 + math.exp(-x))
18 ### END CODE HERE ###
19
TypeError: bad operand type for unary -: 'list'
这次用np.exp()代替math.exp(),然后对向量 ( x 1 , x 2 , … , x n ) \left(x_{1}, x_{2}, \ldots, x_{n}\right) (x1?,x2?,…,xn?)中的每个元素都执行对应的指数运算。
import numpy as np
# example of np.exp
t_x = np.array([1, 2, 3])
print(np.exp(t_x)) # result is (exp(1), exp(2), exp(3))
# 输出[ 2.71828183 7.3890561 20.08553692]
np搞的sigmoid函数
表达式:
?For?
x
∈
R
n
,
?sigmoid?
(
x
)
=
?sigmoid?
(
x
1
x
2
?
x
n
)
=
(
1
1
+
e
?
x
1
1
1
+
e
?
x
2
?
1
1
+
e
?
x
n
)
\text { For } x \in \mathbb{R}^{n}, \text { sigmoid }(x)=\text { sigmoid }\left(\begin{array}{c} x_{1} \\ x_{2} \\ \cdots \\ x_{n} \end{array}\right)=\left(\begin{array}{c} \frac{1}{1+e^{-x_{1}}} \\ \frac{1}{1+e^{-x_{2}}} \\ \cdots \\ \frac{1}{1+e^{-x_{n}}} \end{array}\right)
?For?x∈Rn,?sigmoid?(x)=?sigmoid??????x1?x2??xn???????=?????1+e?x1?1?1+e?x2?1??1+e?xn?1???????
# GRADED FUNCTION: sigmoid
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size
Return:
s -- sigmoid(x)
"""
# (≈ 1 line of code)
# s =
# YOUR CODE STARTS HERE
s = 1/(1 + np.exp(-x))
# YOUR CODE ENDS HERE
return s
t_x = np.array([1, 2, 3])
print("sigmoid(t_x) = " + str(sigmoid(t_x)))
sigmoid_test(sigmoid)
# 输出为sigmoid(t_x) = [0.73105858 0.88079708 0.95257413]
2)sigmoid gradient
通过反向传播(backpropagation)计算梯度来优化损失函数(loss functions)
举个栗子:
sigmoid
?
(
x
)
=
1
1
+
e
?
x
\operatorname{sigmoid}(x)=\frac{1}{1+e^{-x}}
sigmoid(x)=1+e?x1?
s
i
g
m
o
i
d
_
d
e
r
i
v
a
t
i
v
e
(
x
)
=
σ
′
(
x
)
=
σ
(
x
)
(
1
?
σ
(
x
)
)
sigmoid\_derivative(x) = \sigma'(x) = \sigma(x) (1 - \sigma(x))
sigmoid_derivative(x)=σ′(x)=σ(x)(1?σ(x))
其中
σ
(
x
)
\sigma(x)
σ(x)就是sigmoid函数。
# GRADED FUNCTION: sigmoid_derivative
def sigmoid_derivative(x):
"""
Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
Arguments:
x -- A scalar or numpy array
Return:
ds -- Your computed gradient.
"""
#(≈ 2 lines of code)
# s =
# ds =
# YOUR CODE STARTS HERE
s = sigmoid(x)
ds = s * (1 - s)
# YOUR CODE ENDS HERE
return ds
t_x = np.array([1, 2, 3])
print ("sigmoid_derivative(t_x) = " + str(sigmoid_derivative(t_x)))
# 打印sigmoid_derivative(t_x) = [0.19661193 0.10499359 0.04517666]
#sigmoid_derivative_test(sigmoid_derivative)
3)改变多维数组size——image2vector
类似numpy的shape和reshape函数,如果我们要将一张图片,3维矩阵(length,height,depth=3)作为算法的输入时,需要将其形状转为(lengthheight3,1),即将3维张量展开成一维向量。
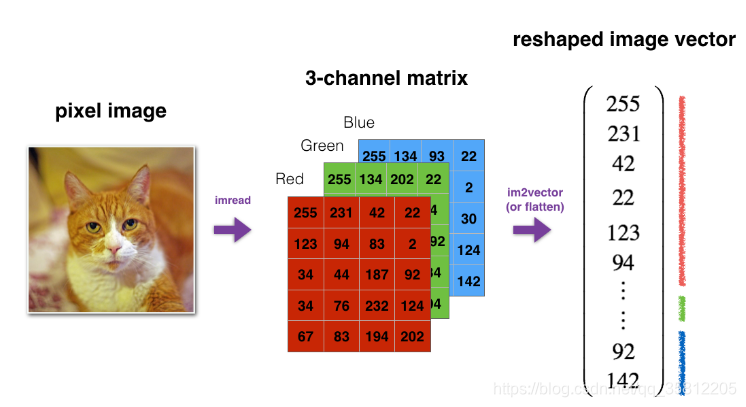
(1)reshape an array v of shape (a, b, c) into a vector of shape (a*b,c)。甚至也可以使用v = v.reshape(-1, 1)。
v = v.reshape((v.shape[0] * v.shape[1], v.shape[2]))
# v.shape[0] = a ; v.shape[1] = b ; v.shape[2] = c
回到一开始的将图片转为向量:
# GRADED FUNCTION:image2vector
def image2vector(image):
"""
Argument:
image -- a numpy array of shape (length, height, depth)
Returns:
v -- a vector of shape (length*height*depth, 1)
"""
# (≈ 1 line of code)
# v =
# YOUR CODE STARTS HERE
v = image.reshape(image.shape[0] * image.shape[1] * image.shape[2], 1)
# YOUR CODE ENDS HERE
return v
# This is a 3 by 3 by 2 array, typically images will be (num_px_x, num_px_y,3) where 3 represents the RGB values
t_image = np.array([[[ 0.67826139, 0.29380381],
[ 0.90714982, 0.52835647],
[ 0.4215251 , 0.45017551]],
[[ 0.92814219, 0.96677647],
[ 0.85304703, 0.52351845],
[ 0.19981397, 0.27417313]],
[[ 0.60659855, 0.00533165],
[ 0.10820313, 0.49978937],
[ 0.34144279, 0.94630077]]])
print ("image2vector(image) = " + str(image2vector(t_image)))
输出结果为:
image2vector(image) = [[0.67826139]
[0.29380381]
[0.90714982]
[0.52835647]
[0.4215251 ]
[0.45017551]
[0.92814219]
[0.96677647]
[0.85304703]
[0.52351845]
[0.19981397]
[0.27417313]
[0.60659855]
[0.00533165]
[0.10820313]
[0.49978937]
[0.34144279]
[0.94630077]]
4)归一化
1.范数
范数包括向量范数和矩阵范数,向量范数表示向量的模(大小),矩阵范数表示矩阵引起变化的大小,前者好理解,后者举例:AX=B将向量X变为B的这个变化大小。
l
p
l_{p}
lp?范数的定义为:
∥
x
∥
p
=
(
∑
i
=
1
n
x
i
p
)
1
p
\|x\|_{p}=\left(\sum_{i=1}^{n} x_{i}^{p}\right)^{\frac{1}{p}}
∥x∥p?=(i=1∑n?xip?)p1?
举栗子:向量x的欧式范数为:
∥
x
∥
2
=
1
2
+
(
?
2
)
2
+
3
2
=
3.742
\|x\|_{2}=\sqrt{1^{2}+(-2)^{2}+3^{2}}=3.742
∥x∥2?=12+(?2)2+32?=3.742
在下面的
n
p
.
l
i
n
a
l
g
.
n
o
r
m
np.linalg.norm
np.linalg.norm的参数ord就表示矩阵的范数:
ord=1:列和的最大值
ord=2:
∣
λ
E
?
A
T
A
∣
=
0
\left|\lambda E-A^{T} A\right|=0
∣∣?λE?ATA∣∣?=0求特征值,然后求最大特征值得算术平方根
ord=正无穷:行和的最大值
2.np.linalg.norm
归一化数据可以使梯度下降得更快。
向量归一化方法:每个行向量除以该行向量的模,举例:
x
=
[
0
3
4
2
6
4
]
x=\left[\begin{array}{lll} 0 & 3 & 4 \\ 2 & 6 & 4 \end{array}\right]
x=[02?36?44?]计算行向量的模长,得到(2,1)的矩阵
∥
x
∥
=
n
p
?.linalg.norm?
(
x
,
?axis?
=
1
,
?keepdims?
=
?True?
)
=
[
5
56
]
\|x\|=n p \text { .linalg.norm }(x, \text { axis }=1, \text { keepdims }=\text { True })=\left[\begin{array}{c} 5 \\ \sqrt{56} \end{array}\right]
∥x∥=np?.linalg.norm?(x,?axis?=1,?keepdims?=?True?)=[556??]
- 如果设置
keepdims=True将会对初始的x进行正确的广播。 - axis=1表示按行进行归一化(使得每行行向量为单位向量),axis=0是按列进行归一化
numpy.linalg.norm还有一个参数ord,用来表示矩阵的范数,其他也可参考:https://numpy.org/doc/stable/reference/routines.array-creation.html
归一化操作:
x
?
normalized?
=
x
∥
x
∥
=
[
0
3
5
4
5
2
56
6
56
4
56
]
x_{-} \text {normalized }=\dfrac{x}{\|x\|}=\left[\begin{array}{ccc} 0 & \dfrac{3}{5} & \dfrac{4}{5} \\ \dfrac{2}{\sqrt{56}} & \dfrac{6}{\sqrt{56}} & \dfrac{4}{\sqrt{56}} \end{array}\right]
x??normalized?=∥x∥x?=????056?2??53?56?6??54?56?4??????
# GRADED FUNCTION: normalize_rows
def normalize_rows(x):
"""
Implement a function that normalizes each row of the matrix x (to have unit length).
Argument:
x -- A numpy matrix of shape (n, m)
Returns:
x -- The normalized (by row) numpy matrix. You are allowed to modify x.
"""
#(≈ 2 lines of code)
# Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, axis = ..., keepdims = True)
# x_norm =
# Divide x by its norm.
# x =
# YOUR CODE STARTS HERE
x_norm = np.linalg.norm(x, axis = 1, keepdims = True)
x = x / x_norm
print(x.shape)
print(x_norm.shape)
# YOUR CODE ENDS HERE
return x
x = np.array([[0, 3, 4],
[1, 6, 4]])
print("normalizeRows(x) = " + str(normalize_rows(x)))
# normalizeRows_test(normalize_rows)
注意上面不要使用x /= x_norm。对于矩阵除法,numpy必须广播x_norm,这是操作符/=不支持的。如下所示的x_norm的shape是(2,1)这个运算过程就用了广播(下面会说)。
结果输出:
(2, 3)
(2, 1)
normalizeRows(x) = [[0. 0.6 0.8 ]
[0.13736056 0.82416338 0.54944226]]
5)广播和softmax function
对于一个(1,n)的向量来说:
?for?
x
∈
R
1
×
n
?
\text { for } x \in \mathbb{R}^{1 \times n} \text { }
?for?x∈R1×n?
softmax
?
(
x
)
=
softmax
?
(
[
x
1
x
2
…
x
n
]
)
=
[
e
x
1
∑
j
e
x
j
e
x
2
∑
j
e
x
j
?
e
x
n
∑
j
e
x
j
]
\begin{aligned} \operatorname{softmax}(x) &=\operatorname{softmax}\left(\left[\begin{array}{llll} x_{1} & x_{2} & \ldots & x_{n} \end{array}\right]\right) \\ &=\left[\begin{array}{llll} \dfrac{e^{x_{1}}}{\sum_{j} e^{x_{j}}} & \dfrac{e^{x_{2}}}{\sum_{j} e^{x_{j}}} & & \cdots & \dfrac{e^{x n}}{\sum_{j} e^{x_{j}}} \end{array}\right] \end{aligned}
softmax(x)?=softmax([x1??x2??…?xn??])=[∑j?exj?ex1???∑j?exj?ex2??????∑j?exj?exn??]?
softmax可看做是分类任务时用到的一个normalizing函数(吴恩达的2nd课有详说)
在斯坦福大学CS224n课程中关于softmax的解释:

对于一个(m,n)的矩阵来说
softmax
?
(
x
)
=
softmax
?
[
x
11
x
12
x
13
…
x
1
n
x
21
x
22
x
23
…
x
2
n
?
?
?
?
?
x
m
1
x
m
2
x
m
3
…
x
m
n
]
\operatorname{softmax}(x)=\operatorname{softmax}\left[\begin{array}{ccccc} x_{11} & x_{12} & x_{13} & \ldots & x_{1 n} \\ x_{21} & x_{22} & x_{23} & \ldots & x_{2 n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{m 1} & x_{m 2} & x_{m 3} & \ldots & x_{m n} \end{array}\right]
softmax(x)=softmax??????x11?x21??xm1??x12?x22??xm2??x13?x23??xm3??……?…?x1n?x2n??xmn????????
=
[
e
x
11
∑
j
e
x
1
j
e
x
12
∑
j
e
x
1
j
e
x
1
3
∑
j
e
x
1
j
?
e
x
1
n
∑
j
e
x
1
j
e
x
2
1
∑
j
e
x
2
j
e
x
22
∑
j
e
x
2
j
e
x
23
∑
j
e
x
2
j
?
e
x
2
n
∑
j
e
x
2
j
?
?
?
?
?
e
x
m
1
∑
j
e
x
m
j
e
x
m
2
∑
j
e
x
m
j
e
x
m
3
∑
j
e
x
m
j
?
e
x
m
n
∑
j
e
x
m
j
]
=\left[\begin{array}{ccccc} \dfrac{e^{x_{11}}}{\sum_{j} e^{x_{1} j}} & \dfrac{e^{x_{12}}}{\sum_{j} e^{x_{1} j}} & \dfrac{e^{x_{1} 3}}{\sum_{j} e^{x_{1} j}} & \cdots & \dfrac{e^{x_{1} n}}{\sum_{j} e^{x_{1} j}} \\ \dfrac{e^{x_{2} 1}}{\sum_{j} e^{x_{2} j}} & \dfrac{e^{x_{22}}}{\sum_{j} e^{x_{2} j}} & \dfrac{e^{x_{23}}}{\sum_{j} e^{x_{2} j}} & \cdots & \dfrac{e^{x_{2 n}}}{\sum_{j} e^{x_{2} j}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \dfrac{e^{x_{m} 1}}{\sum_{j} e^{x_{m} j}} & \dfrac{e^{x_{m 2}}}{\sum_{j} e^{x_{m j}}} & \dfrac{e^{x_{m 3}}}{\sum_{j} e^{x_{m j}}} & \cdots & \dfrac{e^{x m n}}{\sum_{j} e^{x_{m j}}} \end{array}\right]
=?????????????∑j?ex1?jex11??∑j?ex2?jex2?1??∑j?exm?jexm?1??∑j?ex1?jex12??∑j?ex2?jex22???∑j?exmj?exm2???∑j?ex1?jex1?3?∑j?ex2?jex23???∑j?exmj?exm3????????∑j?ex1?jex1?n?∑j?ex2?jex2n???∑j?exmj?exmn???????????????
=
(
softmax
?
(
?first?row?of?
x
)
softmax
?
(
?second?row?of?
x
)
?
softmax
?
(
?last?row?of?
x
)
)
=\left(\begin{array}{c} \operatorname{softmax}(\text { first row of } x) \\ \operatorname{softmax}(\text { second row of } x) \\ \vdots \\ \operatorname{softmax}(\text { last row of } x) \end{array}\right)
=??????softmax(?first?row?of?x)softmax(?second?row?of?x)?softmax(?last?row?of?x)???????
Notes: 后面部分会用m表示number of training examples,and each training example is in its own column of the matrix. Also, each feature will be in its own row (each row has data for the same feature).
Softmax should be performed for all features of each training example, so softmax would be performed on the columns (once we switch to that representation later in this course).
# GRADED FUNCTION: softmax
def softmax(x):
"""Calculates the softmax for each row of the input x.
Your code should work for a row vector and also for matrices of shape (m,n).
Argument:
x -- A numpy matrix of shape (m,n)
Returns:
s -- A numpy matrix equal to the softmax of x, of shape (m,n)
"""
# YOUR CODE STARTS HERE
#Apply exp() element-wise to x. Use np.exp(...).
x_exp = np.exp(x)
# Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
x_sum = np.sum(x_exp, axis = 1,keepdims = True)
# Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
s = x_exp / x_sum
# YOUR CODE ENDS HERE
return s
t_x = np.array([[9, 2, 5, 0, 0],
[7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(t_x)))
# softmax_test(softmax)
上面的x_sum为(2,1)矩阵,x_exp和s均为(2,5)矩阵,通过【广播机制】运算,输出结果为:
softmax(x) = [[9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
1.21052389e-04]
[8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
8.01252314e-04]]
小结:用numpy建立基本函数
- image2vector常用在DL中
- 用np.reshape使矩阵或者向量维度straight将能减少很多bug
- 广播机制
2.向量化
通过数据向量化能大大降低计算的时间复杂度,搞清楚dot/outer/elementwise product的区别。
用传统的for循环:
import time
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
tic = time.process_time()
dot = 0
for i in range(len(x1)):
dot += x1[i] * x2[i]
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
tic = time.process_time()
outer = np.zeros((len(x1), len(x2))) # we create a len(x1)*len(x2) matrix with only zeros
for i in range(len(x1)):
for j in range(len(x2)):
outer[i,j] = x1[i] * x2[j]
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
### CLASSIC ELEMENTWISE IMPLEMENTATION ###
tic = time.process_time()
mul = np.zeros(len(x1))
for i in range(len(x1)):
mul[i] = x1[i] * x2[i]
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
tic = time.process_time()
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
for j in range(len(x1)):
gdot[i] += W[i,j] * x1[j]
toc = time.process_time()
print ("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
三种运算结果,正常的计算时间应该不是0啊。。这个地方有点毛病,后面康康:
dot = 278
----- Computation time = 0.0ms
outer = [[81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.]
[18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[63. 14. 14. 63. 0. 63. 14. 35. 0. 0. 63. 14. 35. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.]
[18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.]
[45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
----- Computation time = 0.0ms
elementwise multiplication = [81. 4. 10. 0. 0. 63. 10. 0. 0. 0. 81. 4. 25. 0. 0.]
----- Computation time = 0.0ms
gdot = [29.69127752 19.45650093 30.14580312]
----- Computation time = 0.0ms
采用向量化计算:
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000 * (toc - tic)) + "ms")
输出结果为:
dot = 278
----- Computation time = 0.0ms
outer = [[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[63 14 14 63 0 63 14 35 0 0 63 14 35 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
----- Computation time = 0.0ms
elementwise multiplication = [81 4 10 0 0 63 10 0 0 0 81 4 25 0 0]
----- Computation time = 0.0ms
gdot = [29.69127752 19.45650093 30.14580312]
----- Computation time = 0.0ms
np.dot()执行矩阵-矩阵 或者 矩阵-向量的乘法运算,他和np.multiply()和*均不相同。
1)L1和L2 loss function
两个loss的定义:
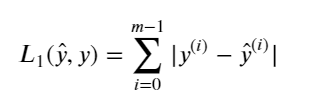
# GRADED FUNCTION: L1
def L1(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L1 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
loss = np.sum(np.abs(yhat - y))
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L1 = " + str(L1(yhat,y)))
>>>
L1 = 1.1
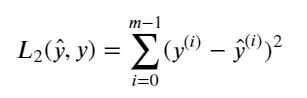
计算平方可以使用np.dot()函数,如果
x
=
[
x
1
,
x
2
,
.
.
.
,
x
n
]
x = [x_1, x_2, ..., x_n]
x=[x1?,x2?,...,xn?],则 np.dot(x,x) =
∑
j
=
0
n
x
j
2
\sum_{j=0}^n x_j^{2}
∑j=0n?xj2?.
# GRADED FUNCTION: L2
def L2(yhat, y):
"""
Arguments:
yhat -- vector of size m (predicted labels)
y -- vector of size m (true labels)
Returns:
loss -- the value of the L2 loss function defined above
"""
### START CODE HERE ### (≈ 1 line of code)
loss = np.dot((yhat - y),(yhat - y).T)
### END CODE HERE ###
return loss
yhat = np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
print("L2 = " + str(L2(yhat,y)))
>>>
L2 = 0.43
Reference
datawhale course