一、统计(机器)学习
? ? ? ? 统计学习就是计算机系统通过运用数据及统计方法提高系统性能的机器学习。
????????统计学习的对象是数据(data)。它从数据出发,提取数据的特征,抽象出数据的模型,发现数据中的知识,又回到对数据的分析与预测中去。作为统计学习的对象,数据是多样的,包括存在于计算机及网络上的各种数字、文字、图像、视频、音频数据以及它们的组合。
????????对数据的预测与分析是通过构建概率统计模型实现的。统计学习总的目标就是考虑学习什么样的模型和如何学习模型,以使模型能对数据进行准确的预测与分析,同时也要考虑尽可能地提高学习效率。
????????统计学习的方法是基于数据构建统计模型从而对数据进行预测与分析。统计学习由监督学习( supervised learning)、非监督学习(unsupervised learning)、半监督学习(semi-supervised learning)和强化学习(reinforcement learning)等组成。
????????统计学习方法:从给定的、有限的、用于学习的训练数据(training data)集合出发,假设数据是独立同分布产生的;并且假设要学习的模型属于某个函数的集合,称为假设空间(hypothesisspace);应用某个评价准则(evaluation criterion),从假设空间中选取一个最优的模型,使它对已知训练数据及未知测试数据(test data)在给定的评价准则下有最优的预测;最优模型的选取由算法实现。
????????统计学习方法包括模型的假设空间、模型选择的准则以及模型学习的算法,称其为统计学习方法的三要素,简称为模型(model)、策略(strategy)和算法(algorithm)。
????????实现统计学习方法的步骤如下:
- 得到一个有限的训练数据集合;
- 确定包含所有可能的模型的假设空间,即学习模型的集合;
- 确定模型选择的准则,即学习的策略;
- 实现求解最优模型的算法,即学习的算法;
- 通过学习方法选择最优模型;
- 利用学习的最优模型对新数据进行预测或分析。
一、基本分类:一般包括监督学习、半监督学习、无监督学习、强化学习、主动学习等
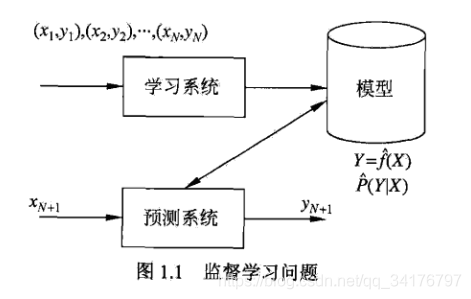
1、监督学习(supervised learning):指从标注数据中学习预测模型的机器学习问题。它的任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测(注意,这里的输入、输出是指某个系统的输入与输出,与学习的输入与输出不同)。它的本质是学习输入到输出的映射的统计规律。
????????监督学习利用训练数据集学习一个模型,再用模型对测试样本集进行预测( prediction)。由于在这个过程中需要训练数据集,而训练数据集往往是人工给出的,所以称为监督学习。监督学习分为学习和预测两个过程,由学习系统与预测系统完成。
?2、无监督学习(unsupervised learning):从无标注数据中学习预测模型的机器学习问题。无标注数据是自然得到的数据,预测模型表示数据的类别、转换或概率。本质是学习数据中的统计规律或潜在规律。模型可以实现对数据的聚类、降维或概率估计。
3、强化学习(reinforcement learning):指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程(Markov decision process)。智能系统能观测到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯策略。
4、半监督与主动学习
? ? ? ? 半监督学习(semi-supervised learning)指利用标注数据和未标注数据学习预测模型的机器学习问题。通常有少量标注数据、大量未标注数据,因为标注数据的构建往往需要人工操作,成本较高;未标注数据的收集不需要太多成本。半监督学习旨在利用未标注数据中的信息,辅助标注数据,进行监督学习,以较低的成本达到较好的学习效果。
? ? ? ? 主动学习(active learning)是指机器不断主动给出实例让教师进行标注,然后利用标注数据学习预测模型的机器学习问题。通常的监督学习使用给定的标注数据,往往是随机得到的,可以看作是被动学习,主动学习的目标是找出对学习最有帮助的实例让教师进行标注,以较小的标注代价,达到较好的学习效果。——知识蒸馏、师生网络
?二、按模型分类
1、概率模型与非概率模型:区别不在于输入输出之间的映射关系,而是模型的内部结构
? ? ? ? 概率模型(probabilistic model):决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型;
? ? ? ? 非概率模型(non-probabilistic model)/ 确定性模型(deterministic model):感知机、支持向量机、K近邻、Adaboost、K均值、潜在语义分析、神经网络。
?2、线性模型与非线性模型 —> 特别是非概率模型
? ? ? ? 如果函数
是线性函数,则称模型是线性模型(linear model),否则是非线性模型。
? ? ? ? 线性模型:感知机、线性支持向量机、K近邻、K均值、潜在语义分析;
? ? ? ? 非线性模型:核函数支持向量机、AdaBoost、神经网络、深度神经网络。
?3、参数化模型与非参数化模型
? ? ? ? 参数化模型假设模型参数维度固定,模型可以由有限维参数完全刻画;非参数化模型假设模型参数的维度不固定或者无穷大,随着训练数据量的增加而不断增大。
? ? ? ? 参数化模型(parametric model):感知机、朴素贝叶斯、逻辑斯谛回归、K均值、高斯混合模型、概率潜在语义分析、潜在狄利克雷分配、潜在语义分析;
? ? ? ? 非参数化模型(non-parametric model):决策树、支持向量机、K近邻、Adaboost。
三、按算法分类
1、在线学习(online learning):每次接受一个样本进行预测,之后学习模型,不断重复该操作的机器学习。——> 有些场景要求学习必须是在线的。比如:数据依次到达无法存储,系统需要及时做出处理;数据规模很大,不可能一次处理所有的数据;数据的模式随时间动态变化,需要算法快速适应新的模式(不满足独立同分布的假设)。——> 很难学到预测准确率更高的模型,每次模型更新中,可利用的数据有限。
2、批量学习(batch learning):一次接受所有数据,学习模型,之后进行预测。
?二、监督学习
1、分类问题
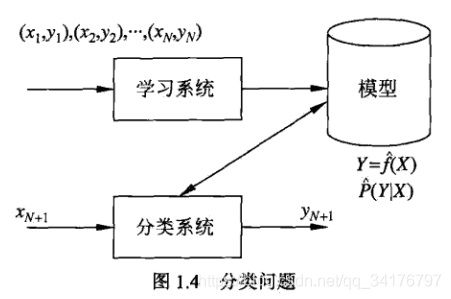
????????分类是监督学习的一个核心问题。在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。这时,输入变量X可以是离散的,也可以是连续的。监督学习从数据中学习一个分类模型或分类决策函数,称为分类器(classifier)。分类器对新的输入进行输出的预测( prediction),称为分类(classification),可能的输出称为类(class)。分类的类别为多个时,称为多类分类问题。
????????分类问题包括学习和分类两个过程。在学习过程中,根据已知的训练数据集利用有效的学习方法学习一个分类器;在分类过程中,利用学习的分类器对新的输入实例进行分类。
????????评价分类器性能的指标一般是分类准确率( accuracy),其定义是:对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。
????????对于二类分类问题常用的评价指标是精确率(precision)与召回率(recall)。通常以关注的类为正类,其他类为负类,分类器在测试数据集上的预测或正确或不正确,4种情况出现的总数分别记作:
- TP—将正类预测为正类数;
- FN—将正类预测为负类数;
- FP—将负类预测为正类数;
- TN—将负类预测为负类数。
*精确率:
*召回率:
*F1值是精确率和召回率的调和均值,即?
,
2、标注问题(tagging)
????????标注( tagging〉也是一个监督学习问题。可以认为标注问题是分类问题的一个推广,标注问题又是更复杂的结构预测(structure prediction)问题的简单形式。标注问题的输入是一个观测序列,输出是一个标记序列或状态序列。标注问题的目标在于学习一个模型,使它能够对观测序列给出标记序列作为预测。注意,可能的标记个数是有限的,但其组合所成的标记序列的个数是依序列长度呈指数级增长的。
????????标注常用的统计学习方法有:隐马尔可夫模型、条件随机场。
????????标注问题在信息抽取、自然语言处理等领域被广泛应用,是这些领域的基本问题。例如,自然语言处理中的词性标注(part of speech tagging)就是一个典型的标注问题;给定一个由单词组成的句子,对这个句子中的每一个单词进行词性标注,即对一个单词序列预测其对应的词性标记序列。
3、回归问题(regression)?
????????回归用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别是当输入变量的值发生变化时,输出变量的值随之发生的变化。回归模型正是表示从输入变量到输出变量之间映射的函数。回归问题的学习等价于函数拟合:选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
????????回归问题按照输入变量的个数,分为一元回归和多元回归;按照输入变量和输出变量之间关系的类型即模型的类型,分为线性回归和非线性回归。
三、无监督学习
????????无监督学习是从无标注的数据中学习数据的统计规律或者说内在结构的机器学习,主要包括聚类、降维、概率估计;可以用于数据分析或者监督学习的前处理。
????????无监督学习的一个困难就是数据没有标注,机器需要自己从数据中找出规律,通常需要大量的数据,因为对数据隐藏的规律发现需要足够的观测。
????????无监督学习的基本想法是对给定数据进行某种“压缩”,从而找到数据的潜在结构。假定损失最小的压缩的带到的结果就是最本质的结构。以矩阵数据为例,发掘数据的纵向机构,把相似的样本聚到同类,即对数据进行聚类;发掘数据的横向结构,把高维空间的向量转换为低维空间的向量,即对数据进行降维;同时对横向和纵向进行处理,假设数据由含有隐式结构的概率模型生成,则可以从数据中学习该概率模型。
1、聚类(clustering)
????????将样本集合中相似的样本(实例)分配到相同的类,不相似的样本分配到不同的类。
????????聚类时,样本通常是欧氏空间中的向量,类别不是事先给定的,而是从数据中自动发现的,但类别的个数通常是事先给定的。类别之间的相似度或距离由应用决定。??
? ? ? ? 如果一个样本只能属于一个类,则成为硬聚类;如果可以属于多个类,则称为软聚类。? ? ??
?2、降维(dimensionality reduction)——> 线性 、非线性
? ? ? ? 将训练数据中的样本从高维空间转换到低维空间。假设样本原本存在于低维空间,或近似地存在于低维空间,通过降维可以更好的表示样本数据的结构(样本之间的关系)。高维空间通常是高维的欧氏空间,而低维空间是低维的欧氏空间或流形(manifold)。低维空间不是事先给定的,是从数据中发现的,其维数通常是事先给定的。从高维到低维中,要保证样本中的信息损失最小。
3、概率模型估计(probability model estimation)——> 概率估计
? ? ? ? 假设训练数据由一个概率模型生成,由训练数据学习概率模型的结构和参数。概率模型的结构类型(集合)事先给定,而模型的具体结构和参数从数据中自动学习。——目标是找到最有可能生成数据的结构和参数。?
四、聚类 —> “物以类聚,人以群分”
聚类,针对给定的样本,依据特征的相似度或者距离,将其归并到若干个“类”或“簇”的数据分析问题;属于无监督学习,只是根据样本的相似度或者距离将其进行归类,而类和簇事先并不知道。
1、相似度 / 距离
? ? ? ? 聚类的对象是观测数据,或样本集合。核心是相似度、距离的定义与选取。
? ? ? ? (1)闵可夫斯基距离 ——> 曼哈顿距离、欧氏距离、切比雪夫距离。
? ? ? ? (2)马哈拉诺比斯距离(Mahalanobis distance),马氏距离
? ? ? ? (3)相关系数:相关系数的绝对值越接近于1,表示样本越相似;越接近0;表示样本越不相似。
? ? ? ? (4)夹角余弦:相关系数的绝对值越接近于1,表示样本越相似;越接近0;表示样本越不相似。
2、类/簇的常用特征
? ? ? ? (1)类的均值:类的中心,其中
表示类中的样本,
表示类G的样本个数。
? ? ? ? (2)类的直径(diameter):类中任意两个样本之间的最大距离
? ? ? ? (3)类的样本散布矩阵(scatter matrix)
? ? ? ? (4)样本协方差矩阵(covariance matrix)
3、类与类之间的距离(连接)
? ? ? ? (1)最短距离(单连接):两个类中样本点之间的最短距离
? ? ? ? (2)最长距离(完全连接):两个类中样本点之间的最长距离
? ? ? ? (3)中心距离:两个类的类中心之间的距离,即两个类样本均值之间的距离
? ? ? ? (4)平均距离:任意两个样本之间距离的平均值
层次聚类——每个样本只属于一个类,硬聚类
? ? ? ? 假设类别之间存在层次结构,将样本聚到层次化的类中。
? ? ? ? 有以下两种:
????????????????(1)聚合(agglomerative)/ 自下而上(bottom-up):开始将每个样本各自分到一个类;之后将相距最近的两类合并,建立一个新类;重复直到满足条件为止;得到层次化的类别结果。
? ? ? ? ? ? ? ? ?(2)分裂(divisive)/ 自上而下(top-down):开始将所有样本分到一个类;之后将已有类中相距最远的样本分到两个新的类,重复此操作直到满足停止条件;得到层次化的类别。
以聚合聚类做分析:
(1)具体过程:对于给定的样本集合,开始将每个样本分到一个类;然后按照一定规则,例如类间距离最小,将最满足规则条件的两个类进行合并;如此反复进行,每次减少一个类,直到满足条件为止。
(2)三要素:距离或相似度的评判标准;类合并规则(一般是类间距最小);停止条件(类个数达到阈值、类的直径超过阈值等)。
(3)示例:聚合聚类算法流程 ——> 复杂度
,m为样本维数,n为样本个数
- 输入:n个样本组成的样本集合及样本之间的距离
- 输出:对样本集合的一个层次化聚类
- 计算n个样本两两之间的欧氏距离,记作D矩阵
- 构造n个类,每个类只包含一个样本
- 合并类间距离最小的两个类,其中使用?最短距离 作为 类间距离,构建一个新类
- 计算新类与当前各类的距离。若类的个数为3,终止计算,否则回到上一步





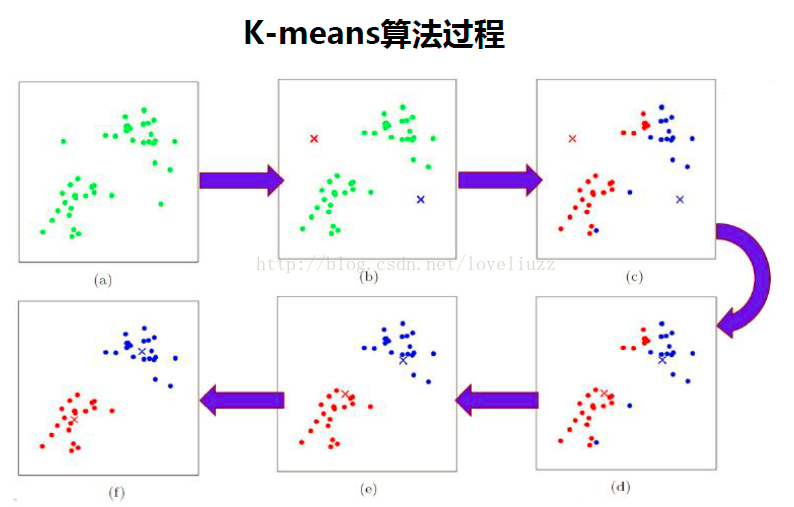





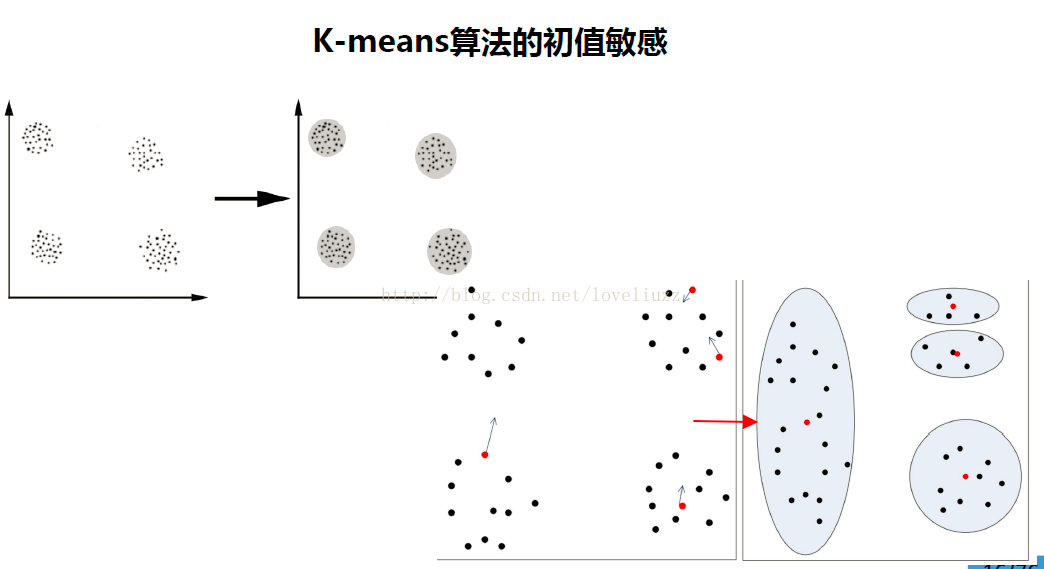

K均值的算法特性
?1、总体特点
? ? ? ? 基于划分的聚类方法;类别数K事先指定;以欧氏距离的平方表示样本之间的距离,以中心(样本的均值)表示类别;以样本和所属类的中心之间的距离总和为最优化的目标函数;得到的类别是平坦的、非层次化的;算法是迭代算法,不能保证得到全局最优。
2、收敛性
? ? ? ? K均值聚类属于启发式方法,不能保证收敛到全局最优;初始中心的选择会直接影响聚类的结果。类中心在聚类的过程中会发生移动,但不会移动太大,因为在每一步中,样本被分到与其最近的中心的类里。
3、初始类的选择
? ? ? ? 选择不同的初始中心,会得到不同的聚类结果。初始中心的选择,比如可以使用层次聚类对样本进行聚类,得到K个类时停止;之后从每个类中选取一个与中心距离最新的点。
4、类别数K的选择 —— 肘部法则(聚类数量选择)
? ? ? ? K均值聚类中的类别数K值需要预先指定,但实际应用中最优的K值是不知道的。一种解决方法:尝试用不同的K值聚类,检验各自得到的聚类结果的质量来推测最优的K值。
? ? ? ? 聚类的质量可以使用类的平均直径来衡量。一般的,类别数变小时,平均直径会增加;类别数变大超过某一值之后,平均直径会保持一个比较稳定(或者不变)的范围;而这个值正是最优的K值。——> 可以使用二分查找,快速定位最优结果。
5、由于没有固定的类别标记,类别的数量和聚类的效果就需要通过肘部法则和轮廓系数进行判断。
- 肘部法则--聚类数量选择
????????肘部法则的计算原理是成本函数,成本函数是类别畸变程度之和,每个类的畸变程度等于每个变量点到其类别中心的位置距离平方和,若类内部的成员彼此间越紧凑则类的畸变程度越小,反之,若类内部的成员彼此间越分散则类的畸变程度越大。在选择类别数量上,肘部法则会把不同值的成本函数值画出来。随着值的增大,平均畸变程度会减小;每个类包含的样本数会减少,于是样本离其重心会更近。但随着值继续增大,平均畸变程度的改善效果会不断减低。值增大过程中,畸变程度的改善效果下降幅度最大的位置对应的值就是肘部。
- 轮廓系数--聚类效果评估
????????轮廓系数是度量类的密集与分散程度,会随着类的规模增大而增大,彼此相距很远,本身很密集的类,其轮廓系数较大;彼此集中,本身很大的类,其轮廓系数较小。
????????好的聚类:内密外疏,同一个聚类内样本要足够密集,不同聚类之间样本要足够疏远。
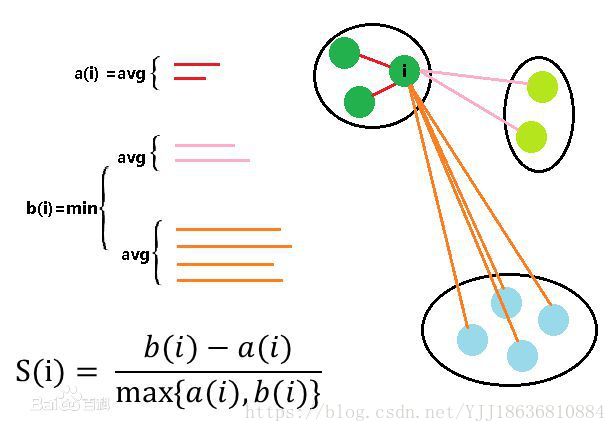
????????轮廓系数计算规则:针对样本空间中的一个特定样本,计算它与所在聚类其它样本的平均距离a, 以及该样本与距离最近的另一个聚类中所有样本的平均距离b,该样本的轮廓系数为(b-a)/max(a, b), 将整个样本空间中所有样本的轮廓系数取算数平均值,作为聚类划分的性能指标s。
????????????????a:某个样本与其所在簇内其他样本的平均距离
????????????????b:某个样本与其他簇样本的平均距离
????????则针对某个样本的轮廓系数s为:?
????????聚类总的轮廓系数SC为:
????????轮廓系数取值范围为:[-1, 1]。 取值越接近1则说明聚类性能越好,相反,取值越接近-1则说明聚类性能越差;0代表聚类重叠,没有很好的划分聚类。
???????? 轮廓系数相关API: import sklearn.metrics as sm
???????????????# v:平均轮廓系数
???????????????# metric:距离算法:使用欧几里得距离(euclidean)
????????????????v = sm.silhouette_score(输入集, 输出集, sample_size=样本数, metric=距离算法)
????????案例:输出KMeans算法聚类划分后的轮廓系数。
三、sklearn中对于kmeans算法的参数