一、神经网络的前向传播原理

在全连接神经网络中，每一层的每个神经元都会与前一层的所有神经元或者输入数据相连，例如图中的 $f _1 ( e )$ 就与 $x_1$ 和 $x_2$ 分别相连。因此，在计算的时候，每一个神经元的输出=使用激活函数激活前一层函数的累加和。
在这里插入图片描述
下面将通过一个具体例子来理解反向传播的具体流程。下图是一个神经网络的结构图，其中：输入数据：i1=0.05，i2=0.10 ;权重系数：w1=0.15，w2=0.20，w3=0.25，w4=0.30，w5=0.40，w6=0.45，- w7=0.50，w8=0.55 ;隐藏层神经元：h1，h2 ;输出层神经元：o1，o2 ;偏置项(bias)：b1=0.35，b2=0.60 ;激活函数：sigmoid
目标：给出输入数据i1, i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
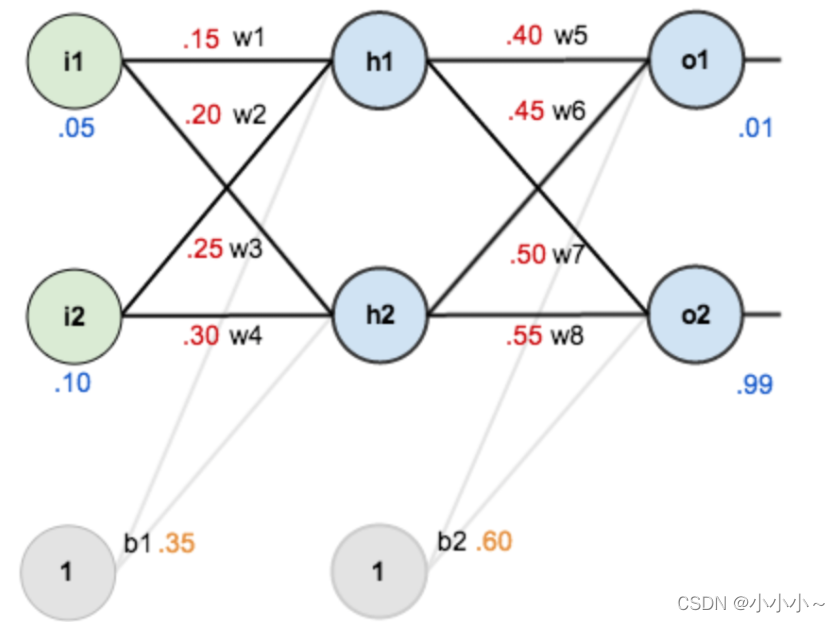
在这里插入图片描述

输入层——>隐藏层
计算神经元h1的加权和 $n e t_{h 1}$ （未经激活函数激活）：
在这里插入图片描述
计算h1的输出 $out_{h1}$ （激活后）：

同理可以计算出h2的输出 $out_{h2}$
在这里插入图片描述
同理可以计算出隐藏层——>输出层

至此前向传播就结束了，我们得到的输出结果是 $out_{o1} =0.75136079 ,out_{o2}=0.772928465]$ , 与目标的[0.01, 0.99]还差的很远。因此，有必要计算误差，更新权重，使预测值接近真实值。

二、神经网络的反向传播原理

Step2 更新输出层权重
由于隐藏层需要将相连接的多个神经元的权重求和，因此为了方便理解，这里先从一个神经元的输出层开始讲解。
1.计算误差
在我们的神经网络中，有两个输出，因此计算误差的时候需要把这两个输出的误差求和。这里计算总误差时，我们采用输出与期望的误差的平方和，即mse的计算方法来计算。
计算误差公式：

在这里插入图片描述
根据此公式，输出1、输出2、总误差的计算如下所示：

2.更新权重
更新权重时，我们需要知道这个权重对全体产生了多少影响，这个影响的大小可以用偏导数求出来。
例：对于输出层权重w5，我们可以用整体的误差对w5求偏导

下图展示了如何使用链式法则来进行反向传播的：
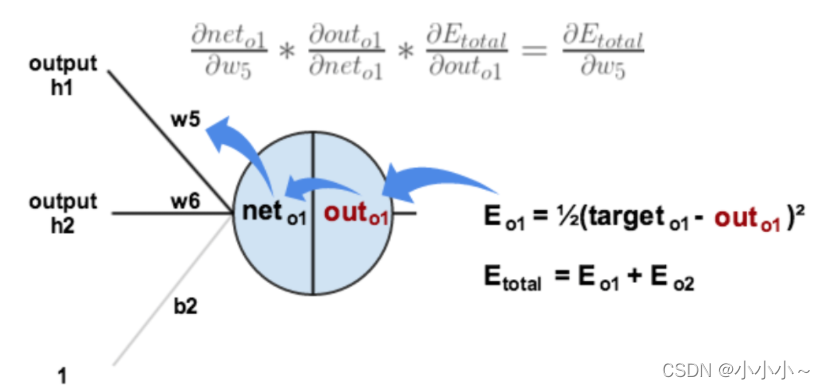
在这里插入图片描述
可以先想象以下有这样的一个函数。 $y = f a (f b (w 0 ， w 1))$ ，在这个函数中，由于是函数的嵌套，没法直接对 $w 0$ 求偏导。想要对 $w 0$ 求偏导的话，需要先用整个函数对外层的 $f_a$ 求偏导，然后在使用 $f_a$ 对 $f_b(w_0, w_1)$ 求偏导。链式法则就是针对这种函数嵌套问题的一种解决方法。（可以理解为套娃，想要求得最里面的偏导数就要一层一层拆开这种感觉。
针对图中的神经元，可以将其想象为以下的嵌套方式 $net_{o1}(w5，w6，w7))$ ，因此为了求得w5对整体误差的影响，需要先用整体误差对 $out_{o1}$ 求偏导，再用 $out_{o1}$ 对 $net_{o1}$ 求偏导，最后使用 $out_{o1}$ 对w5求偏导。
了解了链式法则后，来实际看看使用链式法则对w5来进行求偏导的过程。
具体求解如下：
计算误差公式 $E_{total}/?out_{o1}$
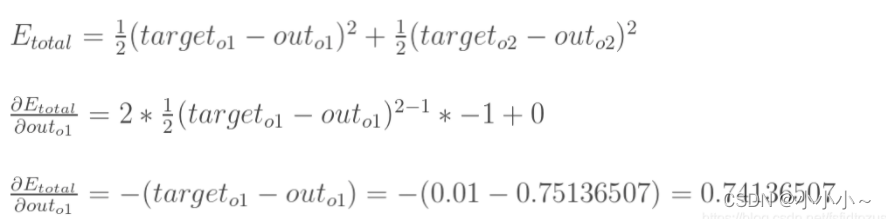
在这里插入图片描述

这一步相当于是对激活函数sigmoid求导

最后三项相乘得到最终的w5的偏导：

在这里插入图片描述
在反向传播中，我们通常使用 $δ$ 来表示误差，因此输出层o1的误差可以表现为 $δ_{o1}$ ,可以表示为如下形式：

因此对于计算w5对整体误差的影响的公式：
在这里插入图片描述
可以表示为：

如果误差为负数，也可以表示成：

根据上面的计算式，来更新w5的权重：

其中η是学习率，这里取0.5,同理更新w6，w7，w8：

Step3 更新隐藏层权重
更新隐藏层的方法，与更新输出层的权重系数的方法类似，但是有一点需要注意。
在更新输出层权重系数w5的时候，我们使用链式法则，通过out(o1)→net(o1)→w5求出。注意！此时神经元o1的求导路径只有一条！
在更新隐藏层权重系数w1，使用链式法则时，通过out(h1)→net(h1)→w1求出，如下：
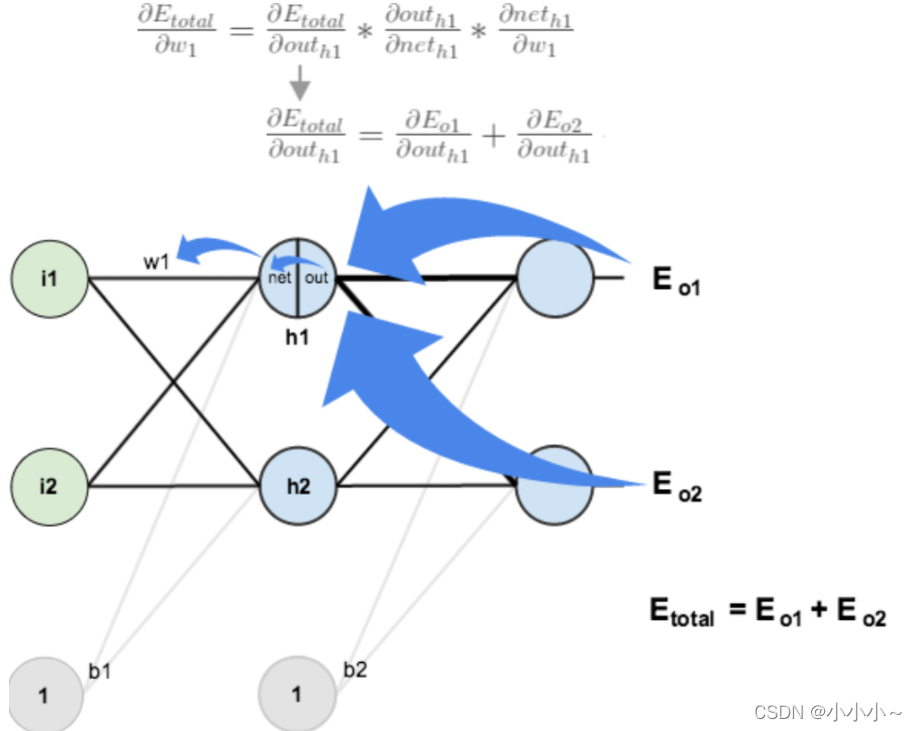
在这里插入图片描述
注意！这个时候神经元o1的求导路径有2条（如蓝色箭头所示）！
因此，计算的时候，需要计算这两个地方传来的误差，并求和:

先计算第一部分的误差：

同理可以计算第二部分：

两者相加计算出总误差：
在这里插入图片描述
再计算数 $\frac{\partial out_{h1}}{\partial net_{h1}}$
计算第3部分的偏导数 $\frac{\partial net_{h1}}{\partial w_{1}}$ ：

三者相乘，计算h1节点对w1的偏导数 $\frac{\partial E_{total}}{\partial w_{1}}$
在这里插入图片描述
至此，就计算出了神经元h1的误差。
将上面的计算步骤整理，可得如下公式：

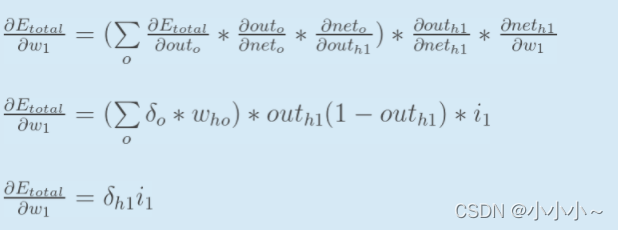
其中，累加符号表示将不同路径的误差相加，此时的路径有两条（图中的两个蓝色箭头）。同时，将计算输出层的误差时说到，计算时使用δ δδ来表示误差，这里的 $δ_{h1}$ 代表神经元h1的误差。得到了神经元h1的误差，就可以根据之前的权重系数以及误差来更新权重系数了。更新h1的权重系数：
在这里插入图片描述

至此，1个神经元的权重系数的更新就完成了。其中的η \etaη代表学习率，通常在程序中指定，可以理解为梯度下降法中的步长。
同理，更新w2,w3,w4的权重系数：
在这里插入图片描述
至此，反向传播就结束了。将这个过程不断重复，就可以不断减小误差，提高正确率，获得比较好的模型了。
感谢博主的知识共享：
原文链接：https://blog.csdn.net/fsfjdtpzus/article/details/106256925